大学数学で一番初めに引っかかりやすいのがイプシロンデルタ論法と呼ばれるものです。
これは、高校でも習う関数の極限値や連続などを、数学的に厳密に定義するときに使う理論となります。
今回はイプシロンデルタ論法を図を使って説明します。
イプシロンデルタ論法とは
イプシロン・デンタ論法($\varepsilon-\delta$論法)とは、関数の極限値について、厳密に定義したものになります。
例えば$\lim_{x\rightarrow c}f(x)=L$は、関数$f(x)$の$x$が$c$に近づいた時の極限値が$L$であることを示しますが、これをイプシロンデルタ論法を使えば、
というふうに定義されます。
記号が読めない方のために簡単に説明をすれば、どんな正の数$\varepsilon$が与えられても、それに対応する$|x-c|<\delta\Rightarrow |f(x)-L|<\varepsilon$が成り立つような正の数$\delta$が存在する(見つけることができる)ということです。
イプシロンとデルタの関係図
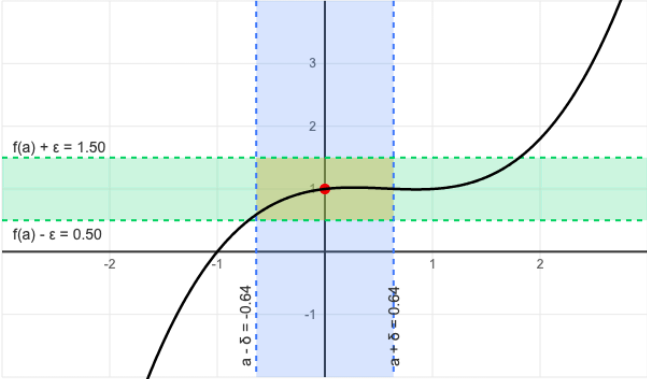
以下の図がイプシロンとデルタの関係になります。
緑がイプシロンの幅、青がデルタの幅になっています。
イプシロンを徐々に小さくしていくと、青の幅も徐々に縮まることがわかります。
イプシロンデルタ論法の定義を確認すると、「$x$ が青にあるならば、$f(x)$ が緑の中に収まる」というような関係を作れば良いことがわかります。
つまり、緑の幅が縮まるにつれて青の幅を十分縮め、その範囲の関数が緑の中に収まるようにすればよいのです。
これが可能かどうかを調べ、可能であればその点が連続・極限であることが言えます。
まとめ
イプシロンデルタ論法は、グラフが得意でなければなかなかイメージが難しい定義です。
$\varepsilon$ の幅を動かして、どのように $\delta$ を選択すれば緑に収まるかを観察してみてください。
あなたにオススメの参考書
イプシロン・デルタ論法を使いこなすための例題がたくさん載っています。今回をきっかけに苦手をなくしておきましょう。
